浅谈计算机浮点数的表示
学过编程的都知道，在计算机中有一种数据类型叫浮点型（float，floating point），用来表示实数集。然而，这种表示只是一种近似表示。例如
0.1 + 0.1 + 0.1 - 0.3
5.551115123125783e-17结果会是5.551115123125783e-17是不精确的。至于为何不精确，这要从浮点数的表示方法说起。目前浮点数的表示遵循的是IEEE754标准。浮点数的表示方法类似于我们学过的科学计数法（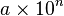
）。不过，科学计数法是以10为底，浮点数的表示是以2为底：a = m × 2e 。尾数m的范围是[1, 2)。指数e的范围是[-1022, 1023]。计算机的字节假设是64位的，那么浮点数中1位表示正负，11位表示指数e ，52位表示尾数m 。以上就是浮点数的表示方法，其大致相当于17位小数的精度。举个例子：0.125 = 1/8 = 2-3,可以用浮点数精确表示。然而，0.1 = 1/10 = ? 这个结果就无法精确表示了。由于浮点数无法精确表示，所以用浮点数来判断是否相等时危险的（b == 0.1 结果会是False）。正确的方法是 abs（b - 0.1）< e ，即判断b 减去0.1差的绝对值是否小于某一个极小的数e 来比较。